栈的顺序存储结构
栈的顺序存储结构
顺序栈:栈的顺序存储,利用一组地址连续的存储单元存放自栈底到栈顶的所有元素,同时附加一个用来指向当前栈顶位置的指针
指针指向栈顶(top)主要是因为栈在线性表的一端操作,操作的那端就是栈顶,方便操作。
顺序栈的存储类型
// 定义栈中元素的最大个数
# define MaxSize 50
// 结构体定义
typedef struct{
ElemType data[MaxSize]; // 存放栈中元素
int top; // 栈顶指针
}SqStack;假设存在顺序栈S,则:
- 栈顶指针:S.top 初始化时设置S.top=-1
- 栈顶元素:S.data[S.top],其中S.top为栈顶指针
- 进栈操作:栈不满时,栈顶指针+1,再送值到栈顶元素
- 出栈操作:栈非空时,先取栈顶元素值,再将栈顶指针-1
- 栈空条件:S.top=-1
- 栈满条件:S.top=MaxSize-1
- 栈长:S.top+1
Tips: 进栈先移动指针,避免占满,元素无法添加,出现外溢;出栈先取栈顶元素,保证指针永远指向栈顶。
顺序栈的存储结构体定义可以很明显看出,顺序栈的入栈操作会受到数组上界(MaxSize)的约束。
当对栈的最大使用空间估计不足时,容易出现栈上溢(外溢),需要主动向用户报告反馈,避免出现错误;
顺序栈的基本运算
InitStack(&S): 初始化一个空栈S,栈顶指针初始化为-1StackEmpty(S): 判断一个栈是否为空,如果栈空则返回true,否则返回falsePush(&S,x): 进栈,若栈未满,x进栈操作,插入到栈内成为新的栈顶元素。Pop(&S,&x): 出栈,若栈非空,出栈操作,弹出栈顶元素,用指针x进行返回。GetTop(S,&x): 读栈顶元素,若栈S非空,用x返回栈顶元素。ClearStack(&S): 销毁栈,释放栈S占用的存储空间。
初始化
InitStack(&S): 初始化一个空栈S,栈顶指针初始化为-1
void InitStack(&S){
// 栈顶指针-1
s.top=-1;
}栈空判断
StackEmpty(S): 判断一个栈是否为空,即:栈顶指针是否为-1,如果栈空则返回true,否则返回false
bool StackEmpty(S){
if(S.top==-1){
// 栈空
return true;
}else{
// 栈非空
return false;
}
}进栈
Push(&S,x): 进栈,若栈未满,x进栈操作,插入到栈内成为新的栈顶元素。
bool Push(SqStack &S,ElemType x){
if(S.top==MaxSize-1){
// 栈满,返回false,元素无法进行进栈操作
return false;
}else{
// 可进栈,栈顶指针+1,再元素入栈
S.data[++S.top]=x;
// 入栈成功
return true;
}
}注意:
- 进栈先移动栈顶指针+1,再操作入栈元素
++i是简写,先对变量i进行递加操作,再进行使用,即:先加后用
出栈
Pop(&S,&x): 出栈,若栈非空,出栈操作,弹出栈顶元素,用指针x进行返回。
bool Pop(SqStack &S,ElemType &x){
if(S.top==-1){
// 栈空,无栈顶元素可出栈,返回false
return false;
}else{
// 栈非空,先元素出栈,再进行指针-1
x=S.data[S.top--];
// 出栈成功,返回true
return true;
}
}注意:
- 出栈操作,先让元素出栈,获取栈顶元素,再移动指针-1
i--是先使用变量i,再对变量做递减操作,即:先用后加(减)
读(获取)栈顶元素
GetTop(S,&x): 读栈顶元素,若栈S非空,用x返回栈顶元素。
bool GetTop(SqStack S,ElemType &x){
if(S.top==-1){
// 栈空,无栈顶元素,返回false
return false;
}else{
// 通过栈顶指针,获取栈顶元素,赋值给变量x
x=S.data[S.top];
// 读取栈顶元素成功,返回true
return true;
}
}上面的这些操作都是基于栈顶指针初始化为-1的情况
当栈顶指针初始化为S.top=0,相关操作操作会有区别:
- 入栈:
S.data[S.top++]=x - 出栈:
x=S.data[--S.top]
同时, 栈空、栈满条件也会有变化,要仔细对比揣摩
共享栈
共享栈:利用栈底位置相对不变的特性,可以让两个顺序栈共享一个一维存储空间,将两个栈的栈底分别设置在共享空间的两端,两个栈顶则向共享空间的中间延伸
Tips: 类似头对头,一致对外这种感觉,噗呲哈哈
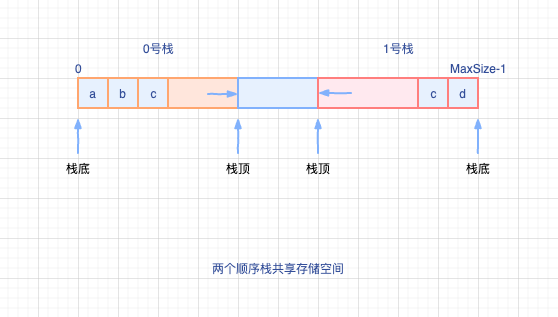
在上面的共享栈结构图中,两个栈(0、1号顺序栈)的栈顶指针都指向栈顶元素
- 0号栈栈顶指针
top=-1时,0号栈为空 - 1号栈栈顶指针
top=MaxSize时,1号栈为空
当且仅当两个栈的栈顶指针相邻(top1-top0=1),可以判断共享栈栈满
进栈
进栈:先移动指针,后进行赋值
- 当0号栈进栈时,0号栈栈顶指针top0
先加1后赋值 - 当1号栈进栈时,0号栈栈顶指针top1
先减1后赋值
出栈
出栈:先进行赋值,后移动指针
- 当0号栈进栈时,0号栈栈顶指针top0
先赋值后减1 - 当1号栈进栈时,0号栈栈顶指针top1
先赋值后加1
共享栈能够更有效的利用存储空间,两个栈空间进行相互调节。只有当这个存储空间(即:共享空间)被占满时才会发生上溢。存取数据的时间复杂度都为O(1),在栈顶操作。
共享栈对存取效率没有什么影响
更新日志
237b3-于84fc0-于
